Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to find the number of connected components in an undirected graph.

Example 1: 0 3 | | 1 --- 2 4 Given n = 5 and edges = [[0, 1], [1, 2], [3, 4]], return 2.

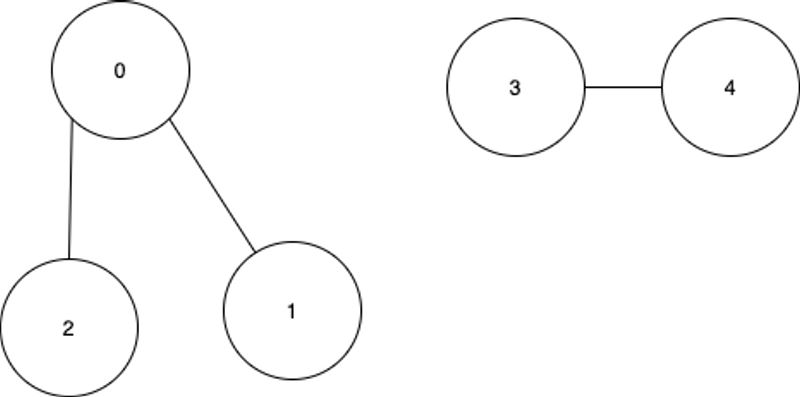
Example 2: 0 4 | | 1 --- 2 --- 3 Given n = 5 and edges = [[0, 1], [1, 2], [2, 3], [3, 4]], return 1.

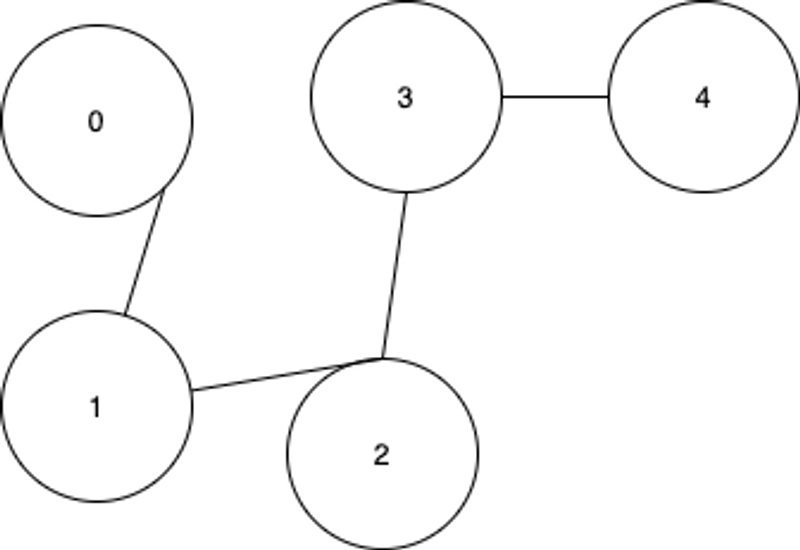
Note: You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

approach union find

• check if the “left” vector has parent if not make it itself
• the second vector parent will be left
  • the compress part makes sure all the “children” vectors point to the root node and can get it in constant time
  • also the diffent number of groups is equal to the response